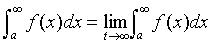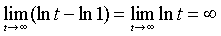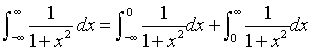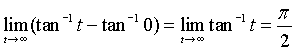tratamos con una función
definida sobre unintervalo finito
y supimos que no tiene una descontinuidad infinita. El consepto de unaintegral definida al caso donde el intervalo es infinito y tambien al caso donde
tiene unadiscontinuidad infinita en
,en uno y otro caso la integral se llama integral impropia.Tipo 1: Intervalos infinitos
Considerar la region infinita, S , que esta bajo la curva 
, sobre el eje x y a la derecha de la
recta x=1. Podria pensarse que como S tiene una extension infinita, su area debe ser infinita; pero examinemos esto con mas cuidado. El area de la parte de S que está a la izquierda de la recta x-t es
, sobre el eje x y a la derecha de larecta x=1. Podria pensarse que como S tiene una extension infinita, su area debe ser infinita; pero examinemos esto con mas cuidado. El area de la parte de S que está a la izquierda de la recta x-t es
Tambien observará que
El area de la región sombreada tiende a 1 cuando
: asi pues, el area de la region infinita, S, es igual a 1. Esto se escribe
Con este ejemplo como guia, definimos la integral de
(no necesariamente un funcion positiva) sobre un intervalo infinito como el limite de integrales sobre intervalos finitos.Definicion de una integral impropia tipo 1
(a) Si esxiste
para todo numero 
, entonces
siempre y cuando exista este limite (como un numero finito)
(b) Si existe
para todo numero 
entonces
siempre que haya este limite (como un numero finito)
Las integrales impropias de
y 
se llaman convergentes si hay tal limite y divergentes si no existe(c) Si
y 
son convergentes, entoces por definicion
Se puede emplear cualquier numero real a en la parte (c).
Cualquiera de las integrales impropias de la definicion 1 se pueden interpretar como una area, siempre que
sea un funcion positiva; por ejemplo, en el caso (a) si 
y la integral 
es convergente, el area de la region 
se define como
es el limite del area bajo la grafica de , de 
a 
cuando
EJEMPLO 1
Determine si la integral
es convergente o divergenteSolución : Segun el inciso(a) de la definicion 1
el limite no existe como numero finito; len consecuencia, la integral impropia es divergente
Comparemos el resultado del ejemplo 1 con el del ejemplo que esta al principio de esta seccion:
convergentes 
divergentesEsto significa, geometricamente, que aunque las curvas
y 
se parecen mucho cuando 
,la regionbajo a la derecha 
tiene un area finita, mientras que la region correspondiente bajo posee area infinita. Observsmos que 
y 
tienden a 0 cuando 
, pero lo hace con mayor rapidez que . los valores de no decrecen lo bastante rapido como para que la integral tenga un valor definidoEJEMPLO 2
Evalue
Solución : Al emplear la parte (b) de la definicion 1, tenemos que
Integramos por partes, haciendo
, de modo que 
y 
sabemos que
cuando 
, de acuerdo con la regal de l'Hospital
Por consiguiente
Evalue
Solucion: Conviene elegii¡r en la definicion 1 (c)
Ahora debemos evaluar por separado las integrales del lado derecho:
como ambas son convergentes, la integral original es convergente y
En vista de que
, la integral impropia dada puede ser interpretada como el area de la region infinita bajo la curva
y arriba del eje XTipo 2:Integrandos sidcontinuos
Sea
una funcion positiva continua, definida en un intervalo finito,
, con una asintota vertical en 
. Sea
la region no acotada bajo la grafica de y sobre el eje X, entre a y b. (Para las integrales de Tipo 1, las regiones se prolongan indefinidamente en direccion horizontal. En este caso, la region es infinita en sentido vertical). El area se la parte entre 
y 
es
es A y se escribe
Esta ecuacion sirve para definir una integral impropia de tipo (2), aun cuando no sea una funcion positiva, sin importar que tipo de discontinuidad tiene
en Definicion de una integral impropia del tipo 2
(a) Si
es continua en y discontinua en si el limite existe, como un numero finito
(b) Si
es continua en y discontinua en 
,
si este limite existe, como un numero finito
La integral impropia se denomina convergente si existe el limite, y divergente si no existe.
(c) Si
tiene una discontinuidad en 
, y 
, y si son convergentes tanto 
como 
por definicion
Ejemplo 1
Determine
Solución: Primero que nada observemos que la integral dada es impropia ya que
tiene la asíntota vertical .
Como la discotinuidad infinita se presenta en el extremo izquierdo de 
, aplicamos la parte (b) de la definición 3 :
Evalúe
Solución : Sabemos que la función
tiene una asíntota vertical en 0 porque 
, por lo tanto, la integral dada es impropia y entonces
Ahora integramos por partes,con
Para determinar el límite del primer término , aplicamos la regla del 1 'hospital:
Por consiguiente,
A veces resulta imposible determinar el valor exacto de una integral impropia, pero es importante saber si es convergente o divergente. En tales casos es posible emplear el siguiente teorema. Aunque lo enunciamos para las integrales del tipo 1 , hay otro similar para las de tipo 2.
Ejemplo 5
Determine
Solución: Primero que nada observemos que la integral dada es impropia ya que
tiene la asíntota vertical .
Como la discotinuidad infinita se presenta en el extremo izquierdo de 
, aplicamos la parte (b) de la definición 3 :
Por consiguiente , la integral impropia del problema es convergente.
Ejemplo 2
Indique si
converge o diverge.
Solución : Notará que la integral dada es impropia, pues
. Al emplear e inciso (a) de la definición 3 tenemos que
Ejemplo 2
Indique si
converge o diverge.Solución : Notará que la integral dada es impropia, pues
. Al emplear e inciso (a) de la definición 3 tenemos que
Ya que 
y 
cuando 
así pues ,la integral impropia original es divergente.
Ejemplo 3
Evalúe
de ser posible.
Solución : la recta
es una asíntota vertical del integrado. Como se presenta a la mitad del intervalo 
, usaremos la parte (c) de la definicion 3, con c=1;
y 
cuando 
así pues ,la integral impropia original es divergente.Ejemplo 3
Evalúe
de ser posible.Solución : la recta
es una asíntota vertical del integrado. Como se presenta a la mitad del intervalo 
, usaremos la parte (c) de la definicion 3, con c=1;
en donde 
Porque 
cuando 
. Por lo tanto , 
es divergente. Esto quiere decir que 
es divergente .
Precaución De no adverti la asíntota en el ejemplo 3 , quizá habriamos confundido la integral con una ordinaria y ejecutando este cálculo erroneo:
Esto esta mal , ya que la integral es impropia y se debe calcular en términos de límites.
De ahora en adelante , cuando encuentre el simbolo
debe decidir, examinado la función 
en 
, si es una integral definida ordinaria o una integral impropia.
Ejemplo 4
cuando 
. Por lo tanto , 
es divergente. Esto quiere decir que 
es divergente .
Precaución De no adverti la asíntota
en el ejemplo 3 , quizá habriamos confundido la integral con una ordinaria y ejecutando este cálculo erroneo:
Esto esta mal , ya que la integral es impropia y se debe calcular en términos de límites.
De ahora en adelante , cuando encuentre el simbolo
debe decidir, examinado la función en 
, si es una integral definida ordinaria o una integral impropia.Ejemplo 4
Evalúe
Solución : Sabemos que la función
tiene una asíntota vertical en 0 porque 
, por lo tanto, la integral dada es impropia y entonces
Ahora integramos por partes,con
Para determinar el límite del primer término , aplicamos la regla del 1 'hospital:
Por consiguiente,
Prueba de comparación para integrales impropias
A veces resulta imposible determinar el valor exacto de una integral impropia, pero es importante saber si es convergente o divergente. En tales casos es posible emplear el siguiente teorema. Aunque lo enunciamos para las integrales del tipo 1 , hay otro similar para las de tipo 2.
Ejemplo 5
P<1>
